什么是快速排序?
快速排序算法遵循分而治之的方法。它根据一定的条件将元素划分为较小的部分,并对这些划分的较小部分执行排序操作。
快速排序算法是所有编程语言中最常用和最流行的算法之一。但是,如果是J,要理解这一点,首先我们需要知道什么是排序,JavaScript中的默认排序是什么。
什么是分类?
排序只不过是按照我们想要的顺序排列元素。就像将数字从小到大(升序)或从大到小(降序)排列一样,这就是我们到现在所看到的,称为排序。
JavaScript中的默认排序
如前所述,javascript具有 sort() 。让我们举一个没有元素数组(如[5,3,7,6,2,9])的示例,并希望只需对Items数组调用 sort() ,它就会按升序对数组元素进行排序。
代码:
在javascript中选择快速排序而不是默认 sort() 的原因是什么
虽然 sort() 给出了我们想要的结果,但问题出在它对数组元素进行排序的方式上。JavaScript中的默认 sort() 使用ChromeV8引擎的插入排序和Mozilla Firefox和Safari的合并排序。
但是,如果需要对大量元素进行排序,则不适用于其他情况。因此,解决方案是对大数据集使用快速排序。
因此,要完全理解,需要了解Quick Sort是如何工作的,现在让我们详细了解一下。
什么是快速排序?
快速排序遵循分而治之的算法。它是根据一定的条件将元素分成更小的部分,然后执行SO,以下是快速排序的步骤,用简单的话说就是。
- 首先选择一个要称为透视元素的元素。
- 接下来,将所有数组元素与选定的轴心元素进行比较,并以这样的方式排列它们:小于轴心元素的元素在其左侧,大于轴心元素的元素在其右侧。
- 最后,对左侧元素和右侧元素执行与透视元素相同的操作。
这就是快速排序的基本轮廓。以下是执行快速排序需要逐个遵循的步骤。
快速排序是如何工作的?
- 首先在数组中找到“Pivot”元素。
- 左指针从数组的第一个元素开始。
- 从数组的最后一个元素开始右指针。
- 将指向左的元素与左指针进行比较,如果它小于透视元素,则将左指针向右移动(在左索引上加1)。继续执行此操作,直到左侧元素大于或等于枢轴元素。
- 将指向右的元素与右指针进行比较,如果它大于透视元素,则将右指针向左移动(右索引减去1)。继续执行此操作,直到右侧元素小于或等于枢轴元素。
- 检查左指针是否小于或等于右指针,然后查看这些指针位置中的元素。
- 递增左指针,递减右指针。
- 如果左指针的索引仍然小于右指针的索引,则重复该过程;否则返回左指针的索引。
那么,让我们用一个例子来看看这些步骤。让我们考虑需要排序的元素数组是[5,3,7,6,2,9]。
确定透视元素
但在继续进行快速排序之前,选择轴心元素起着重要作用。如果选择这样做,建议始终选择中间元素(数组长度除以2)作为枢轴元素,我们也是这样做的。
以下是执行快速排序的步骤,如示例[5,3,7,6,2,9]所示。
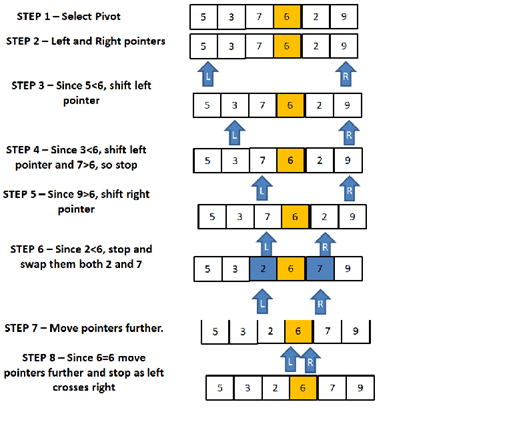
第一步:确定枢轴为中间元素。因此,7是枢轴元素。
步骤2:将左指针和右指针分别作为数组的第一个和最后一个元素开始。因此,左指针指向索引0处的5,右指针指向索引5处的9。
第三步:将左指针处的元素与透视元素进行比较。因为,5<6将左指针向右移位到索引1。
步骤4:现在,仍然是3<6,所以将指针向左移动到向右多一个索引。所以现在7>6停止递增左指针,现在左指针在索引2处。
步骤5:现在,将右指针处的值与Pivot元素进行比较。现在,当2<6时,停止移动右指针。
步骤6:将左指针和右指针上的两个值互换。
步骤7:将两个指针再移动一步。
步骤8:由于6=6,将指针再移动一步,当左指针穿过右指针时停止,并返回左指针的索引。
因此,在这里,基于上面的方法,我们需要编写用于交换元素和对数组进行分区的代码,如上面的步骤所述。
在JavaScript中交换两个数字的代码:
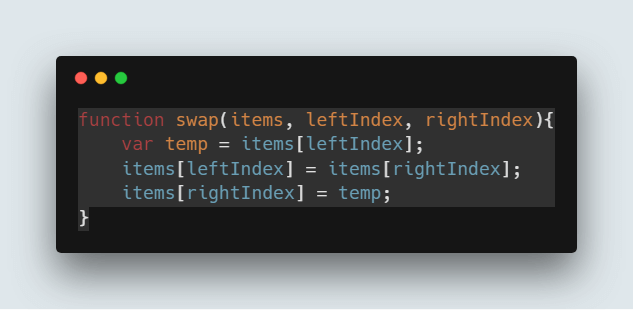
function swap(items, leftIndex, rightIndex){
var temp = items[leftIndex];
items[leftIndex] = items[rightIndex];
items[rightIndex] = temp;
}执行上述步骤中所述分区的代码:
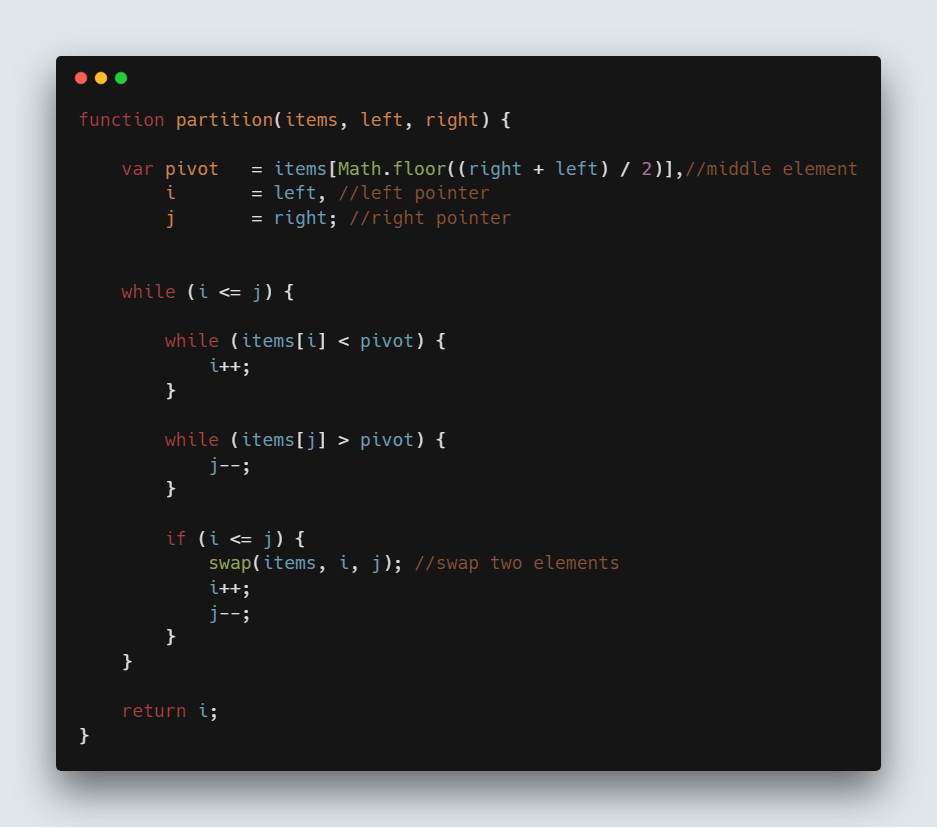
function partition(items, left, right) {
var pivot = items[Math.floor((right + left) / 2)], //middle element
i = left, //left pointer
j = right; //right pointer
while (i <= j) {
while (items[i] < pivot) {
i++;
}
while (items[j] < pivot) {
j--;
}
if (i <= j) {
swap(items, i, j); //swap two elements
i++;
j--;
}
}
return i;
}执行递归操作
一旦执行上述步骤,将返回左指针的索引,我们需要使用它来划分数组并对该部分执行快速排序。因此,它被称为分而治之算法。
因此,将执行快速排序,直到对左数组和右数组上的所有元素进行排序。
注意:快速排序是在同一数组上执行的,在此过程中不会创建新的数组。
因此,我们需要将其称为上面解释的 partition() ,并在此基础上将数组划分为多个部分。所以这是使用它的代码,
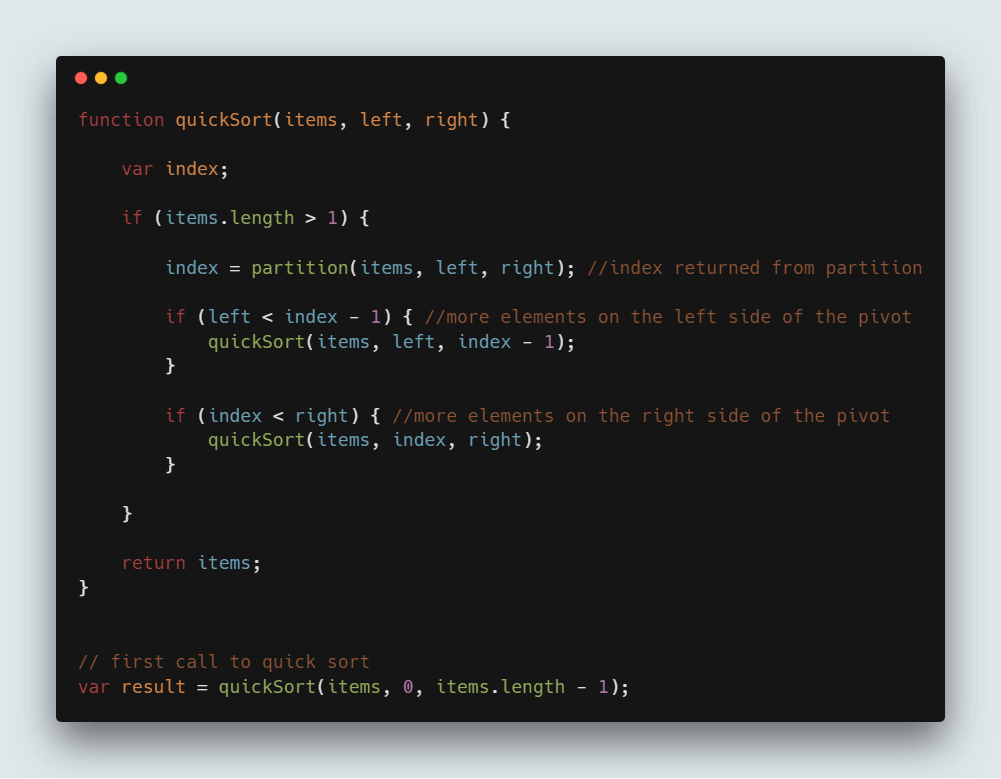
function quickSort(items, left, right) {
var index;
if (items.length > 1) {
index = partition(items, left, right); //index returned from partition
if (left < index - 1) { //more elements on the left side of the pivot
quickSort(items, left, index - 1);
}
if (index < right) { //more elements on the right side of the pivot
quickSort(items, index, right);
}
}
return items;
}
// first call to quick sort
var result = quickSort(items, 0, items.length - 1);完整的快速排序代码:
var items = [5,3,7,6,2,9];
function swap(items, leftIndex, rightIndex){
var temp = items[leftIndex];
items[leftIndex] = items[rightIndex];
items[rightIndex] = temp;
}
function partition(items, left, right) {
var pivot = items[Math.floor((right + left) / 2)], //middle element
i = left, //left pointer
j = right; //right pointer
while (i <= j) {
while (items[i] < pivot) {
i++;
}
while (items[j] > pivot) {
j--;
}
if (i <= j) {
swap(items, i, j); //sawpping two elements
i++;
j--;
}
}
return i;
}
function quickSort(items, left, right) {
var index;
if (items.length > 1) {
index = partition(items, left, right); //index returned from partition
if (left < index - 1) { //more elements on the left side of the pivot
quickSort(items, left, index - 1);
}
if (index < right) { //more elements on the right side of the pivot
quickSort(items, index, right);
}
}
return items;
}
// first call to quick sort
var sortedArray = quickSort(items, 0, items.length - 1);
console.log(sortedArray); //prints [2,3,5,6,7,9]
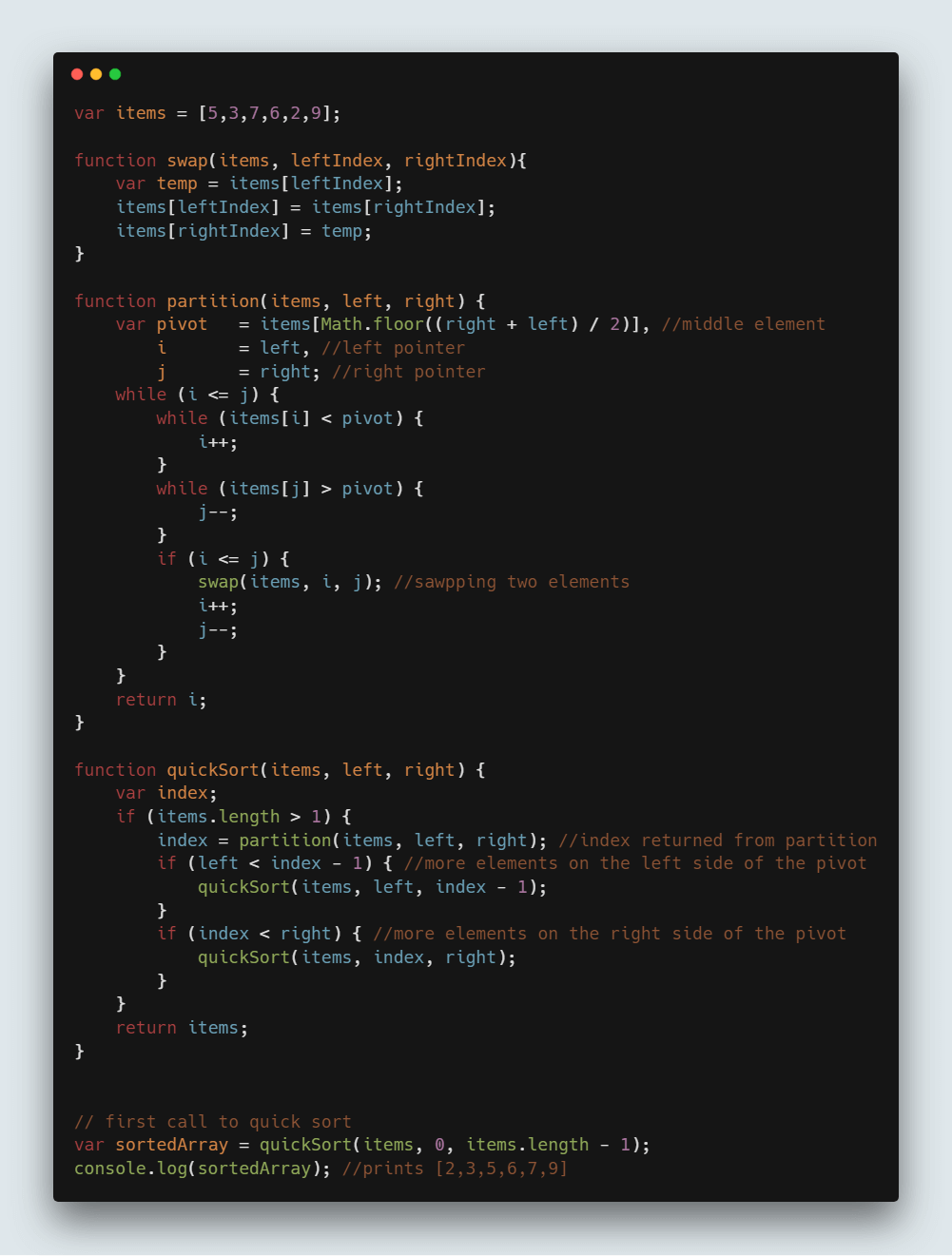
注意:快速排序以 O(nlogn) 的时间复杂度运行。